Updated to electronic spectroscopies.
Interaction of molecules with radiation
Three types of interactions
- Absorption
- Stimulated emission
- Spontaneous emission
Depending on situations, the rate of one process may dominate.
Einstein’s coefficients
The coefficients describing the rate of the above processes.
- The term is the energy density of the radiation, a function of frequency.
- Note that:
- The coefficient is like a 2nd order rate constant;
- The coefficient is like a 1st order rate constant.
where the term is the transition dipole moment.
A and B coefficients are related
At equilibrium,
Assuming:
- Black body radiation - density given by Planck law. .
- Non-degenerate Boltzmann distribution of population. .
Then, rearranging gives
Note: The rate of spontaneous emissions increases drastically with frequency, i.e. energy gap. This is as expected.
- Microwave: sp.em. often very slow, not important.
- UV/VIS: sp.em. often dominant - so we usually record absorption spectra.
Line width
The line width is most commonly described by width at half maximum, .
- Sometimes, the line width is limited by the instrument.
- Otherwise, the width could be the fundamental property of the sample or the experimental method.
Broadening is usually due to the fact that the molecules spend a finite amount of time in any particular energy level. The uncertainty relationship is
Put into frequency units,
Natural broadening
This is due to spontaneous emission.
The spectroscopy lifetime is taken as , so the line width is
- Excited electronic states ~.
- Rotational states ~.
Pressure (collision) broadening
The mean time between collisions can be estimated by gas kinetic therory.
It can be worked out that
- Dominant contribution in microwave
- Important contribution in IR.
Doppler broadening
(This is not related to lifetime.)
Molecules travel in random orientations, so the speed of different molecules is different relative to the lightbeam.
Doppler broadening is
- proportional to frequency - tend to be dominant for VIS.
- IR ;
- VIS .
- proportional to sqrt of temperature.
Application
Taking all these into consideration, to achieve the best resolution, the supersonic jet molecular beam can be used.
Compressed through a small aperture, into a vacuum chamber. The detector is at right angles to the jet.
- All energies converted to translational energy in one direction - at lowest levels for other motions.
- Same direction, same speeds - very rare collision.
- Right angles observation - no Doppler shift.
- BUT, only low concentration possible, hence weak signals.
Rotational spectroscopy
Types of rotating molecules
In this context, the three axes defined w.r.t. moments of inertia are always in the order
Spherical tops:
- High symmetry, e.g. or .
Symmetric tops
With axis or axis.
- Prolate: , e.g. .
- Oblate: , e.g. .
Asymmetric tops
(Linear molecules) - a special case of prolate top.
Energy levels
The following formula could be derived from operator point of view.
For symmetric tops, two quantum numbers are specified:
- - magnitude of total angular momentum as . .
- - angular momentum about the unique axis as . .
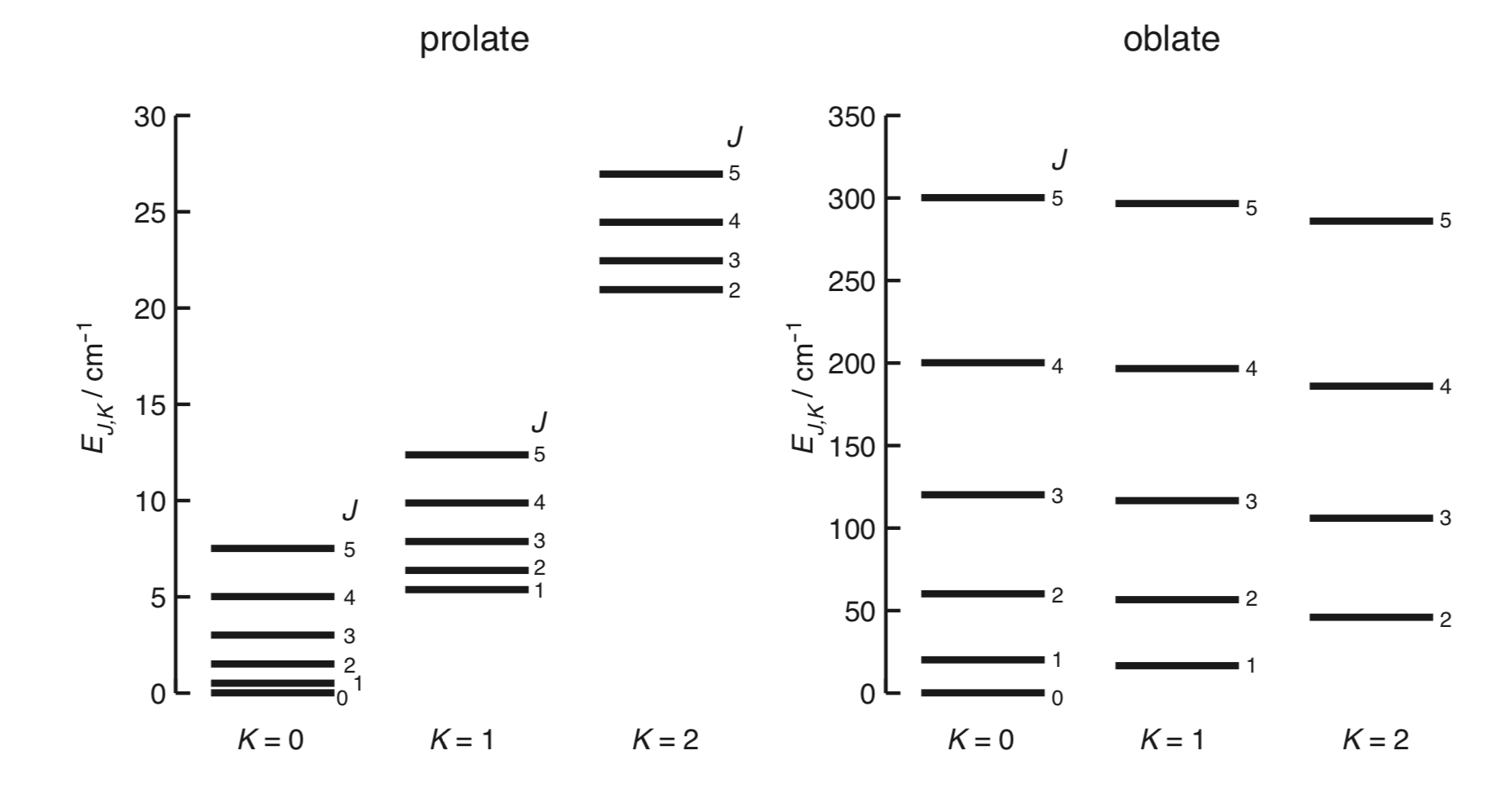
Prolate top
The energy levels are
where the rotational constants are
Remember .
Or in wavenumber units,
with
Oblate top
A plot for typical values.
Spherical top and linear molecules
Both have the same energy levels
Selection rules
- As always, a permanant dipole is needed.
- . Photon has 1 unit of angular momentum.
- . Changing the rotation about the unique axis does not change the dipole, hence not allowed.
Spectra
Symmetric tops
Since , the energy difference is as linear molecules.
- Lines starting from
- Lines apart
Intensities
Before, only the population difference and the ground state degeneracy is considered, but also involved are factors including -dependence of the Einstein coefficients.
Before
Full
This full prediction is quite good.
Centrifugal distortion
As molecules rotates faster, the forces on the atoms will cause the bonds to stretch and bond angles to change.
- Moments of inertia should now depend on .
- However, for simplicity, the improvement is added to the energy levels.
For prolate tops,
The s are very small, typically .
For linear diatomics, it can be shown that
Change in spectra
Now the lines are
- All lines move to lower frequencies.
- Now are separated.
Stark effect
The effect where application of a field results in a splitting of energy levels. (Here only electric field is concerned.)
- The dipole moment may be worked out from the splittings.
- Information about values can help assigning the spectra.
Derivation on pp. 34-35 Keeler (2019).
The quantum number is the angular momentum projected onto the E field.
Change in spectra
- A transition will split into lines.
- The splitting between adjacent lines is .
Vibrational spectroscopy
Deriving the HO selection rule
HO eigenfunctions
Remember that in the reduced coordinates, the HO Hamiltonian is
The eigenfunctions are
where the is a Hermite polynomial.
The eigenfunctions are mutually orthogonal.
Ladder operators
Define the operators
and it can be shown that
Note that we can write
Transition dipole moment
As appeared before in the Einstein coefficients, the transition dipole moments is given by
Note that the dipole moment is a function of internuclear separation, hence the scaled coordinate . An expansion about gives
- The integration over the constant term is only non-zero if , due to the orthonormality of eigenfunctions.
Hence, , the gross selection rule i.e. the dipole must change as the internuclear separation changes from equilibrium position.
Now look at the integral of itself.
For a non-zero integral, , which is the HO selection rule .
Symmetry of wavefunctions
Non-degenerate
- Even transforms as totally symmetric representation
- Odd transforms as the symmetry of the normal mode
Degenerate
- GS transforms as totally symmetric
- 1st excited transforms as the symmetry of the normal mode
- Afterwards use direct product table, and take the symmetric representations
Only use symmetric, since the wavefunctions are symmetric w.r.t. exchange of vibrational quanta.
Example. .
For linear molecules regarding the bending modes, there is vibrational angular momentum (quantum number ) associated.
- Takes value , in steps of 2.
- Energies slightly different (a few ), so lines split.
- The levels can be labelled with .
Fermi resonance
If two levels (nothing to do with transitions) are close in energy, they mix and ‘push each other apart’.
This has consequence on
- frequencies, transitions to and from both levels are changed
- intensities, e.g. an overtone can ‘borrow’ intensity from a fundamental when the two relevant levels mix.
Transitions
It is also convenient to label the overall state of all modes in the form , and the transitions
Fundamental
- From: GS of all modes
- To: 1st excited of 1 of the modes
- Need: symmetry of the mode matches x, y or z
If the fundamental transition of a mode is allowed, it is IR active.
Overtone
- From: GS of all modes
- To: 2nd excited of 1 of the modes
- Allowed due to anharmonicity
Hotbands
- Transitions from other than GS
- Temperature dependent
Linear molecules
The allowed transitions are in two types
- Parallel transitions. Transition dipole along . e.g. transitions.
- Perpendicular transitions. Transition dipole along . e.g. transitions.
Rotational Fine Structure
Linear molecules
Parallel
Selection rules
| Branch | |
|---|---|
| R | |
| P |
For transitions, sometimes a very weak branch is seen.
Perpendicular
| Branch | |
|---|---|
| R | |
| 0 | Q |
| P |
Symmetric tops
Parallel
Require:
except .

Complications
- Centrifugal distortion terms - transitions with different values do not overlap.
- Require , so the larger the the more missing lines.
Perpendicular
Require:
Now for each , there are , and branches for each. Fortunately, only branches are resolved.
so the branch lines are apart.

Labels:
| Label | |
|---|---|
| +1 | |
| -1 |
Intensities
- Upper vibrational levels are hardly populated, hence GS population is dominant.
- Nuclear spin effect.
Raman Spectroscopy
The 4th interaction between molecules and radiation is scattering. The type of spectroscopy using scattering is Raman spectroscopy.
Theory
Semi-classical description
- Electric field of the laser induces a dipole in the molecule.
- The induced dipole oscillates at the same frequency as the laser. (c.f. driven oscillation)
- The anisotropy in polarizability modulates the size of induced dipole (w.r.t. time).
- Oscillating dipole emits EM waves, which.
- has a base frequency of the incident laser
- amplitude modulated by the oscillation of polarizability (e.g. rotation speed).
Quantum description
Need the idea of a virtual state.
The relationships between the energy levels and the wave frequencies is
Rotational Raman
Linear molecules
The selection rules are
This gives the lines (Stokes) at
- The first line at .
- Subsequent lines spaced by .
- Gives O (anti-Stokes) and S (Stokes) branches.
Symmetric tops
The selection rules are
- Additional lines at intervals.
Spherical tops
No rotational Raman, because of the isotropic polarizability.
Vibrational Raman
- Need change in polarizability during vibration. The mode transforms as a product of two coordinates.
- For HO, .
The anti-Stokes lines are very weak in this case, because the upper vibrational level is barely populated.
Rotational fine structures
The fine strucure branches are centered at the vibrational scattered lines, not the laser line.
O, Q and S branches are seen, and the method of combination difference can be used to calculate rotational constants.
Modes and features
Intensity:
- Breathing modes, e.g. A1 modes (all atoms stretch together - large change in polarizability), give very strong scatterings.
- Bending modes give weak scatterings.
Polarization:
Depolarization ratio: .
- Totally symmetric modes give polarized scattering - .
- Otherwise, bands are depolarized - .
Electronic Spectroscopy
PE curves
Potential energy curves plot the energies vs the internuclear distance.
- Each excited state has a unique PE curve
- Different states may dissociate into different atomic states
- Curves with different symmetries can cross each other
Selection rules
They can be expressed in terms of parts of the term symbol:
- If involving heavier atoms, the spin selection rule may not hold.
There is no limit in the vibrational energy.
For rotational transitions:
- Almost always see absorption spectra, because electronic transitions are too high in energy; similarly absorption from is usually seen.
- Discharge or flame can give rise to emission spectra. Collisions can degrade vibrational energy, so still emission from is usually seen.
Vibrational Course Structure
Draw out the two curves, and the energy difference should be obvious.
- A progression is a series of transitions with a common energy level.
- A sequence is a seires of transitions with a common .
Intensity and FC factor
In the transition dipole moment expression, vibrational part can be separated. In an electronic transition, the light interacts with the electronic wavefunction only, so does not operate on .
Now the vibrational integral describes the overlap between the upper and lower vibrational wavefunctions. Define the Franck-Condon factor
- Centre of the GS need to overlap with the asymmetric part of the upper state to have a large integral - usually the edge of wavefunctions.
For absorption spectra
| Change in | Overlap with upper curve | Spectra |
|---|---|---|
| Decrease | At the shallow end | Several high strong |
| 0 | At GS | Strong |
| Increase | At the steep end | Many high strong |
Classical interpretations of FC factor
The electronic transition itself is very fast compared to the motion of atoms, so the nuclei are expected to have the same position and momentum after the transition.
- At GS, classically there is 0 momentum.
- Same nuclear position means a vertical transition.
- Zero momentum means at the turning points.
Dissociation
Dissociation can be observed in the spectra, if the FC factor is in favour. The lines converge until the dissociation limit where the lines become a continuum.
For an absorption spectra:
| Upper curve | Overlap with upper curve | Spectra |
|---|---|---|
| Smaller | At the shallow end | Transitions close to the limit can be observed |
| Larger | At the steep end | The limit continuum can be observed |
| Cross a repulsive curve | radiationless transition into the repulsive curve | Pre-dissociation can be observed, which usually has a lifetime broadening |
Measurement of dissociation energies
It is very unlikely that the vibration GS and the dissociation limit of a curve are both obsered in the spectrum. Hence, Birge-Sponer extrapolation is used.
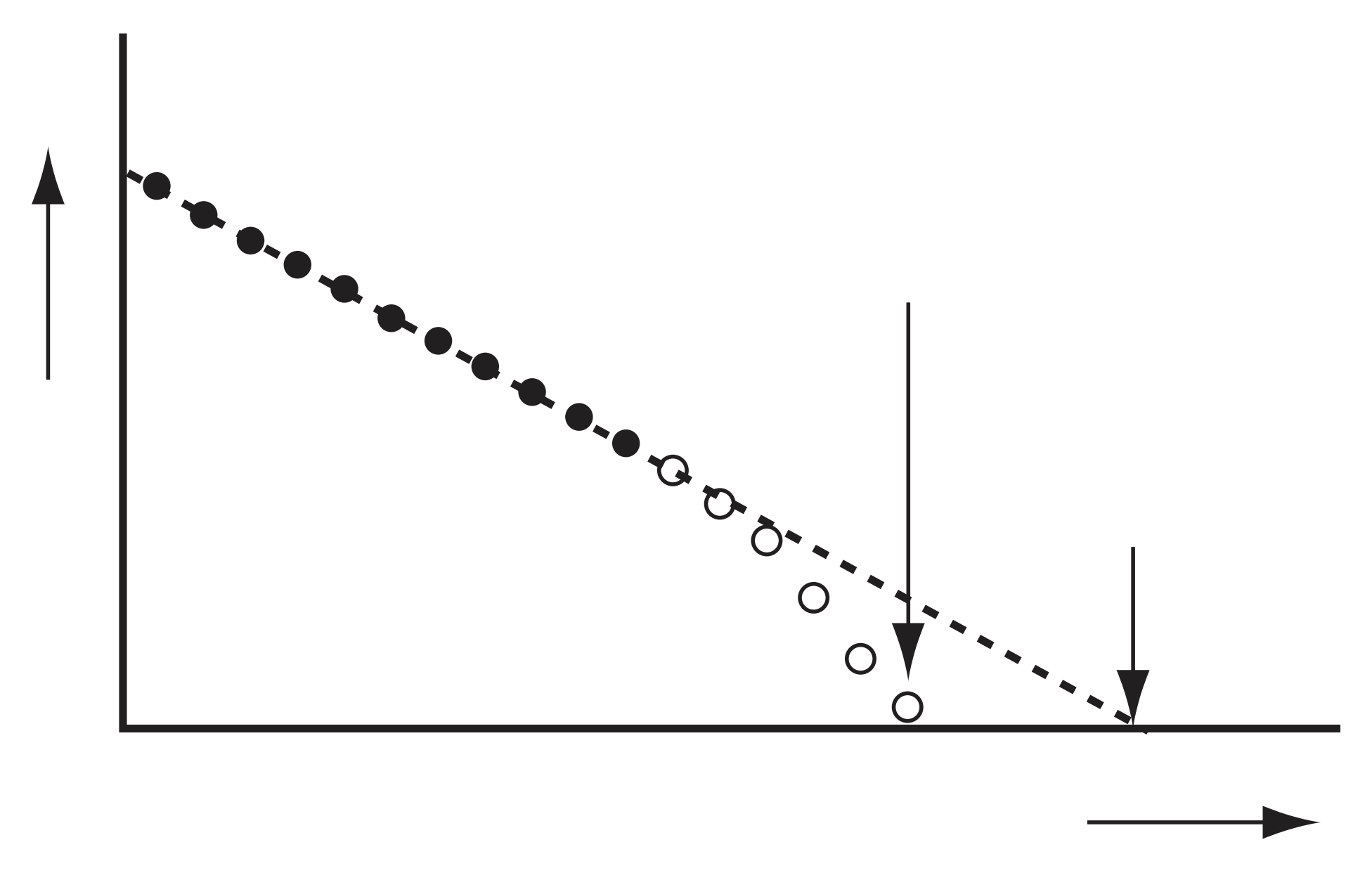
- X-axis plots .
- Y-axis plots the energy difference between and levels, labelled . (Note that the is the argument, not an multiplication).
- Now, dissociation energy is the sum of energy differences between levels, hence the area under graph.
- For a Morse potential, the graph should be a straight line.
- However, the real data exhibits curving, hence the is overestimated by using Morse.
- Curving can be due to charge separation, etc.
Deslandres table
It is hard to make sure the assignments in the electronic spectra are correct. Use Deslandres tables for this purpose.
| 0 | 1 | 2 | |||
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 |
- Label as columns and as rows.
- Fill in the assigned wavenumbers.
- The differences between the adjacent columns or rows should be the same.
Rotational fine structures
Remember the exact positions of lines depend on the rotational constants of both upper and lower levels.
For vib-rot transitions, and are only very slightly different. But for different electronic states, the hence can be very different.
| P branch | R branch | |
|---|---|---|
| Further apart | Closer together R band head Degraded to the red |
|
| Closer together P band head Degraded to the blue |
Further apart |
The position of the band head can be calculated by differentiating the relevant or expressions.