Cambridge IB Chemistry course with some IB Physics blended in.
Ionic Model
In the lattice, ions experience the force from neighbours, next-neighbours, next-next-neighbours, …, forming a conditionally convergent series.
The sum is (or rather from experimental data is deduced to be) Madelung constant, \(\mathcal{A}\). Therefore the energy can be expressed as a function of lattice spacing \(a\) to be \[ E=-\frac{N_A \mathcal{A}z_{+}z_{\_}e^2}{4\pi\epsilon_0 a}+\frac{B}{a^n}. \] The repulsive term usually have \(n\) of 9-12.
Extremising this expression gives \[ U_0=-\frac{N_A \mathcal{A}z_{+}z_{\_}e^2}{4\pi\epsilon_0 a_0}(1-\frac{1}{n}) \] and generally approximates that \(\Delta H_{latt}\approx-U_0\).
Reciprocal lattice
It is the Fourier transform of the real lattice - a lattice in \(k\) space.
Construction
No need to do FT. For real lattice vectors \(\mathbf{a}_i\) and reciprocal lattice vectors \(\mathbf{b}_i\), \[ \mathbf{a}_i\cdot\mathbf{b}_i=2\pi\delta_{ij}.\\ \] In 3D (usually in…), \[ \mathbf{b}_3=\frac{2\pi(\mathbf{a}_1\times\mathbf{a}_2)}{[\mathbf{a}_1,\mathbf{a}_2,\mathbf{a}_3]} \] Maybe useful: volume of reciprocal unit cell \(\Omega=(2\pi)^3/V_c\).
Brillouin zones
Construction
- Arbitrarily choose an origin in the reciprocal space
- Connect this point to all other lattice points with line segments
- Draw out the perpendicular bisectors of every line segment
- Walk from the origin, in straight lines, and every time you cross a besector line, the zone number +1.
Properties
- Each BZ has the same area / volume = \(\Omega\).
- Since the origin is arbitrarily chosen, and the lattice has translation symmetry, any zone can be mapped onto the 1st zone. (folding)
Free electron gas
Idea
- Consider only valence electrons
- Electrons are free to move within the lattice
- There is no potential due to nuclei, or electron-electron interactions
- Pauli principal applies
Hamiltonian and B.C.
Free particle, so \[ \hat{H}=-\frac{\hbar^2}{2m_e}\frac{d^2}{dx^2}. \] The eigenfuntion and eigenvalue are \[ \psi=e^{ikx}\\ E=\frac{k^2\hbar^2}{2m_e} \] To quantise this, BvK boundary condition is used - the phase at one end of the crystal is continuous with that at the other end, i.e. \[ k(N_x a)=n2\pi \] where \(a\) is unit cell length and \(N_x\) is the number of unit cells along the direction.
Thus the quantisation restriction on \(k\) is \[ k=n(\frac{2\pi}{N_x a}). \tag{1}\label{k} \] States are uniformly spaced in \(k\) space.
Density of states
It is more useful (later on) to consider the density of \(k\) states. \[ D=\frac{\mathrm{No. \ of\ states}}{\mathrm{Length \ in \ k \ space}}=\frac{1}{\mathrm{spacing}}=\frac{N_x a}{2\pi}=\frac{\mathcal{L}}{2\pi} \] The \(\mathcal{L}\) is called BvK length.
The same idea can be extended to 2D and 3D - with respective BvK area and BvK volume. \[ D_{2D}=\frac{N_x N_y A_\mathrm{cell}}{(2\pi)^2}=\frac{\mathcal{A}}{(2\pi)^2}\\ D_{3D}=\frac{N_x N_y N_z V_\mathrm{cell}}{(2\pi)^3}=\frac{\mathcal{V}}{(2\pi)^3} \]
Fermi-Dirac distribution
Why not Boltzmann
Compared to translation of molecules,
- Electrons are much lighter, so the energy spacing is wider;
- The number density is much higher in the solid than gas phase.
Therefore, number of states is no longer much larger than number of particles, and hence there are states whose occupation greatly exceeds 1.
Due to Pauli principal, this is not possible, so another distribution is needed.
Fermi-Dirac
Due to a restriction on ‘box size’ (i.e. Pauli in the case of electrons), each state is filled with max 2 electrons, and they are filled up to a level way way way higher than \(kT\) (at ambient temperatures).
The distribution has the form \[ F(E)=\frac{1}{\exp((E-\mu)/kT)+1} \] where \(\mu\) is the chemical potential, or Fermi level. To a good approximation, \(\mu\) can be replaced with \(E_F\), the Fermi energy.
Fermi level and energy
Fermi energy is straightforward - the highest level filled at absolute zero. No excess energy for any excitation, so the cut off is sharp and well-defined.
At non-zero temperature, the cutoff is no longer sharp, and Fermi level is the level with exactly 50% probability of being filled. It is therefore temperature dependent.
They are often used interchangeably.
Strictly, for systems with density of states increasing with energy, Fermi level is lower than Fermi energy.
Limits
At high energy limit, \(\exp((E-\mu)/kT)\gg 1\), so \(F\to \exp(-E/kT)\), i.e. Boltzmann.
Density of states in terms of energy
Idea: (at absolute 0) the actually number of electrons = 2 * number of states up to Fermi energy.
In 3D:
First define total number of electrons up to \(E\) \[\begin{align} W(E)&=2\times \mathrm{Volume}\times\mathrm{Density\ of\ states} \\ &=2\times\frac{4}{3}\pi k^3\times\frac{\mathcal{V}}{(2\pi)^3}\\ &=\frac{k^3\mathcal{V}}{3\pi^2}\\ &=\frac{\mathcal{V}}{3\pi^2}(\frac{2m_e E}{\hbar^2})^\frac{3}{2}\\ &\propto E^\frac{3}{2} \end{align}\] Equal to actual number of electrons at \(E=E_F\) to find \[\begin{align} &W(E)=n_e \mathcal{V}\\ \implies &\begin{cases}k_F=(3\pi^2n_e)^\frac{1}{3}\\ E_F=\frac{\hbar^2}{2m_e}(3\pi^2n_e)^\frac{2}{3} \end{cases} \end{align}\] We can also now calculate density of states in terms of energy \[\begin{align} D(E)&=\frac{d}{dE}W(E)\\ &=\frac{\mathcal{V}}{2\pi^2}(\frac{2m_e }{\hbar^2})^\frac{3}{2}E^\frac{1}{2} \end{align}\] and average energy of the states (up to Fermi energy) \[ <E>=\frac{\int_0^{E_F}E\cdot D\,dE}{\int_0^{E_F} D\,dE}=\frac{3}{5}E_F \]
A lot of other quantities
Heat Capacity
A very approximate way
- Only electrons within about \(kT\) of the Fermi energy is promoted
- There are \(N\times \frac{kT}{E_F}\) of these
- They have approximately \(kT\) energy each
So the total internal energy and heat capacity are \[ U=kT\times (N\times \frac{kT}{E_F})\\ C_{V,m}=\frac{d U}{dT}=\frac{2RkT}{E_F}=\frac{2R}{T_F}T \] where the Fermi temperature is defined to be \(E_F/k\).
Physics Way
- Only electrons within about \(kT\) of the Fermi energy is promoted
- There are \(D(E_F)kT\) of these
- Treating classically, each electron has \(3kT/2\) energy
This gives \[ C=\frac{9}{2} \frac{Nk}{T_F}T \] Just a constant out.
Formal way
Carefully integrating the exact expressions. \[ U=\int_0^\infty E\cdot D(E)\cdot F(E)\,dE\\ \implies C\approx \frac{\pi}{2}\frac{Nk}{T_F}T \] Still only a constant out. Heat capacity proportional to temperature.
Bulk Modulus
This property has a quantum origin.
When the metal is squashed, the volume decreases, which means that the energy spacing increases, (recall \(\ref{k}\)), and the total energy increases. Therefore, the metal is resistant to external pressure.
Electron pressure \[ p=-\frac{\partial U}{\partial V}=-\frac{\partial }{\partial V}(\frac{3}{5}\frac{\hbar^2}{2m_e}(3\pi^2n_e)^\frac{2}{3})=\frac{2}{5}Nc\mathcal{V}^{-\frac{5}{3}}(=\frac{2}{5}nE_F) \] Then, the bulk modulus is defined to be \[\begin{align} B&=\frac{\mathrm{pressure}}{\mathrm{fraction\ change\ in\ volume}}\\ &=-V\frac{\partial p}{\partial V}\\ &=-V\frac{\partial }{\partial V}\frac{2}{5}NcV^{-\frac{5}{3}}\\ &=\frac{2}{3}Nc\mathcal{V}^{-\frac{5}{3}}\\ &=\frac{2}{3}nE_F \end{align}\]
Electrical conductivity
Electron motion
- Electrons collide with electrons, defects and phonons
- The mean time between collisions is \(\tau\)
- Assume after collision, the speed is 0
- Assume an exponential distribution for probability of collision
\[ <\!\!v\!\!>=v\exp(-\frac{t}{\tau})\\ \implies\frac{d<\!\!v\!\!>}{dt}=-\frac{<\!\!v\!\!>}{\tau} \]
Equation of motion
\[ m^*(\frac{d\mathbf{v}}{dt})=-e\mathbf{E}-e\mathbf{v}\times\mathbf{B}-m^*\frac{\mathbf{v}}{\tau} \]
The last term is the drag term due to collisions.
The drift velocity is defined such that the drift term and the electric field term cancels: \[ m_e^*\frac{\mathbf{v_d}}{\tau}=-e\mathbf{E}. \] The electron mobility is defined as \[ \mu=\frac{v_d}{E}=\frac{e\tau}{m_e^*}. \]
Current density
Then current density can be easily worked out: \[\begin{align} j&=\frac{\mathrm{charge}}{\mathrm{time}\times\mathrm{area}}\\ &=\frac{n_ev_d\Delta t A e}{\Delta t A}\\ &=n_e v_d e\\ (&=n_ee\mu E) \end{align}\] We get \(j=\sigma E\propto E\), so Ohm’s law is obeyed.
Conductivity can be read off as \[ \sigma=\frac{j}{E}=n_e e \mu. \]
Interpretation
- External field shifts the Fermi sphere opposite to its direction.
- Constant field gives a constant shift velocity.
- But collisions prevents it from shifting indefinitely.
- In reality, the shift turns out to be tiny compared to the size of Fermi sphere.
Therefore, the resulting average of the electron momentum is no longer 0, but opposite to the field direction.
Note: Since the density of states is high, there are always free states available right next to the occupied states - hence the conduction in metal is not an activated process.
Scattering
Scattered electrons need to go into a new available state. Both phonon and defect scattering can only produce a large change in momentum but not energy, which means changes direction, but not radius. Hence only possible to occur near Fermi sphere (otherwise there are no free states with similar radii).
The states in the front is scattered more strongly (due to higher energy), hence on average, scattering tries to push the Fermi sphere back to the origin.
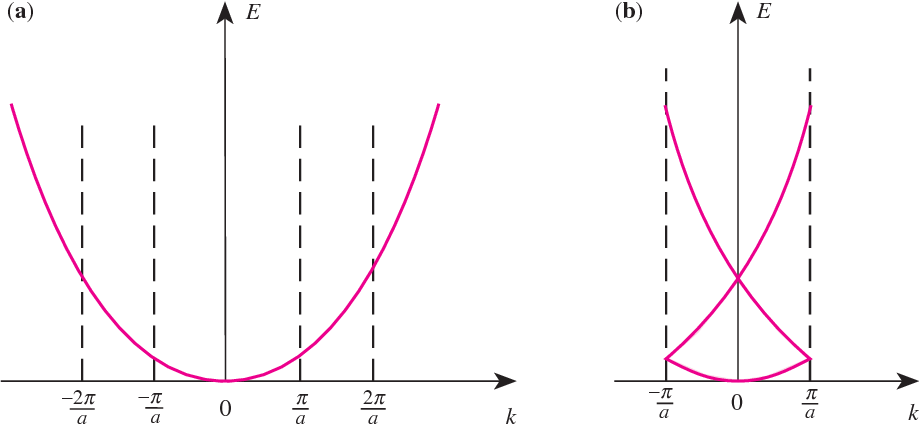
Nearly-free electron gas
Now we take into account some weak interactions with the lattice - so only need to make some slight adjustments to the FEG model.
