IB Spectroscopy Techniques

Notes Chemistry

Word count: 643Reading time: 4 min

 2019/03/15  178  Share

Overall picture

Scale

Type	Energy scale / $\pu{cm-1}$	EM wave
Electronic	10000	UV/VIS, X-ray
Vibration	1000	IR
Rotation	1	Microwave

Requirements

Rotation (Microwave) Spectra
- Need permanent dipole
- x, y or z transforms as totally symmetric representation
Infrared
- Need change in dipole upon vibration
- Corresponding normal modes transform like x, y or z
Raman
- Need change in polarisability
- Complementary to IR
  1. Rotation: detectable except spherical caps (eg $\ce{CH4}$ , $\ce{SF6}$ )
  2. Vibration: corresponding normal modes transform like any coordinate squared term

Unit conversion

Just remember: wavenumber = $1/\lambda$ , everything follows

Energy $E=h\nu=hc/\lambda=h\tilde{c}\tilde{\nu}$ in Joule

But quantity in Joule is not equal to quantity in $\pu{cm-1}$ .

Rotation

Derived from the Schrödinger equation for rigid rotors.

Key quantities

Quantity	Formula
Energy	$E=hBJ(J+1)$
Rotational constant	$B=\frac{\hbar^2}{2I}$	in J
	$\tilde{B}=\frac{h}{8\pi^2\tilde{c}I}$	in $\pu{cm-1}$
Degeneracy	$2J+1$

$J$ gives the amount of angular momentum
$M_J$ specifies the direction of anuglar momentum

Form of spectrum

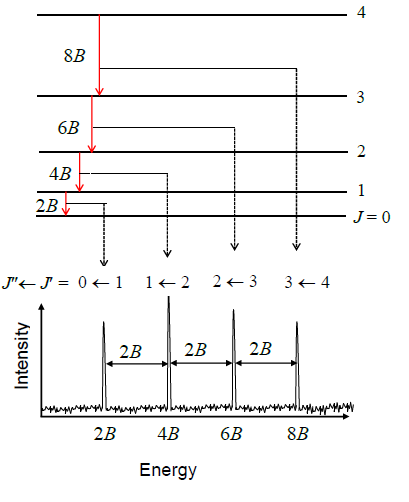
Intensity

Population of levels

Generally, population obeys Boltzmann distribution:

N_{J} = N_{0} exp (- \frac{h ~ c ~ B J (J + 1)}{k T})

$N_J=N_0\exp(-\frac{h\tilde{c}\tilde{B}J(J+1)}{kT})$

This combined with degeneracy,

p o p u l a t i o n \propto (2 J + 1) exp (- \frac{E_{J}}{k T})

$\mathrm{population}\propto(2J+1)\exp(-\frac{E_J}{kT})$

Factors affecting intensity

As stimulated emission can happen at the same time as absorption, the intensity depends on population differences (instead of population of the lower state).
Transition dipole moment $<\!\!\psi_1|\mu|\psi_2\!\!>$ .

Max populated level

Obtained by differentiation of the population expression. Result is $J_{max}\approx\sqrt{\frac{kT}{2h\tilde{c}{\tilde{B}}}}-\frac{1}{2}$ .

Transition requirements

Must have permanent dipole
During transition $J$ must change by $\pm1$ . This is due to the photon having 1 unit of angular momentum.

Polyatomic linear

Same form, just more complicated in calculating $I$ .

Isotopic substitution

Substituting an isotope changes - obviously- the mass, but does not change bond length significantly. This is because:

The potential energy curve does not change
Only the ZPE changes (slightly), hence gives a very slightly different $<r>$ , or $<1/r^2>$ if calculating $I$ .

Hence, the bond lengths can be calculated by solving simultaneous equations.

Rotation Raman

Raman

The electric field of the photon induces a dipole in the molecule
The molecule promoted to a virtual state
The molecule re-emits a photon

If:

$\begin{align} h\nu'=hv && E'=E && \mathrm{Rayleigh \ scattering} \end{align}\\ \begin{cases} h\nu'<h\nu & E'>E&& \mathrm{Stoke \ scattering}\\ h\nu'>h\nu & E'<E && \mathrm{anti-Stoke \ scattering} \end{cases}$

For Rayleigh, since photons are indistinguishable, we don’t know whether a photon is absorbed and re-emitted or straight through.

Selection Rule

$\Delta J=0, \pm2$

Example spectrum

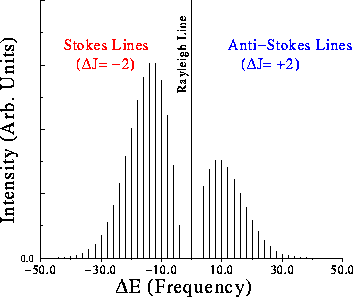
Vibration spectrum

Harmonic oscillator

Key quantities

Quantity	Formula
$\mu$	$\frac{m_1m_2}{m_1+m_2}$
$\nu$	$\frac{1}{2\pi}\sqrt{\frac{k}{\mu}}$	in Hz
$\epsilon$	$(v+\frac{1}{2})\tilde{\omega}$	in $\pu{cm-1}$

Selection rule

$\Delta \nu=\pm1$

Anharmonic Oscillator

The Morse potential takes the form:

$V_M(x)=D_e[1-\exp(-\beta x)]^2$

Quantity	Formula
$k_M$ - spring constant	$2D_e\beta^2$	obtained by Taylor expansion
$E_v$	$(v+\frac{1}{2})\hbar\omega-(v+\frac{1}{2})^2\hbar\omega x_e$	in Joules - this is exact
$\epsilon_v$	$(v+\frac{1}{2})\tilde{\omega}-(v+\frac{1}{2})^2\tilde{\omega} x_e$	in $\pu{cm-1}$
$x_e$	$\frac{\hbar\beta^2}{2\mu\omega}$
$D_e$		Depth of well
$D_0$	$D_e-E_0$	Dissociation energy
$\beta$		Steepness of well

The $E-v$ curve is parabolic - the points beyond the energy start to decrease in energy, which are non-physical. $v_{max}$ can be obtained by differentiating energy w.r.t $v$ .

$v_{max}=\frac{1}{2x_e}-\frac{1}{2}\\ \tilde{D}_e=\frac{\tilde{\omega}}{4x_e} \\$

Transitions

Must have change in dipole during vibration
Selection rule is less strict, $\Delta v=\pm1,\pm2, \pm3...$ . The curve is no longer symmetric, so integrals no longer vanishing.

Important transitions

Fundamental - $0\to1$ - strong
1st overtone - $0\to2$ - weak
Hot band - $1\to 2$ - weak, temperature dependent

Vibrating rotor

For a simultaneous change of both vibrational energy and rotational energy in a diatomic molecule:

$\Delta v=\pm1,\pm2,\pm3 ...\\ \Delta J=\pm1$

Notations

Rot state for lower vib state $J''$

Rot state for upper vib state $J'$

Lines for $\Delta J$	-2	-1	0	1	2
	O	P	Q	R	S

Combination difference

As $v$ changes, $<r>$ (also $<1/r^2>$ ) changes, $I$ changes, hence $B$ is different for upper and lower vibration states.

Nevertheless they can be solved by combination difference method - using transitions of the same upper state or same lower state.

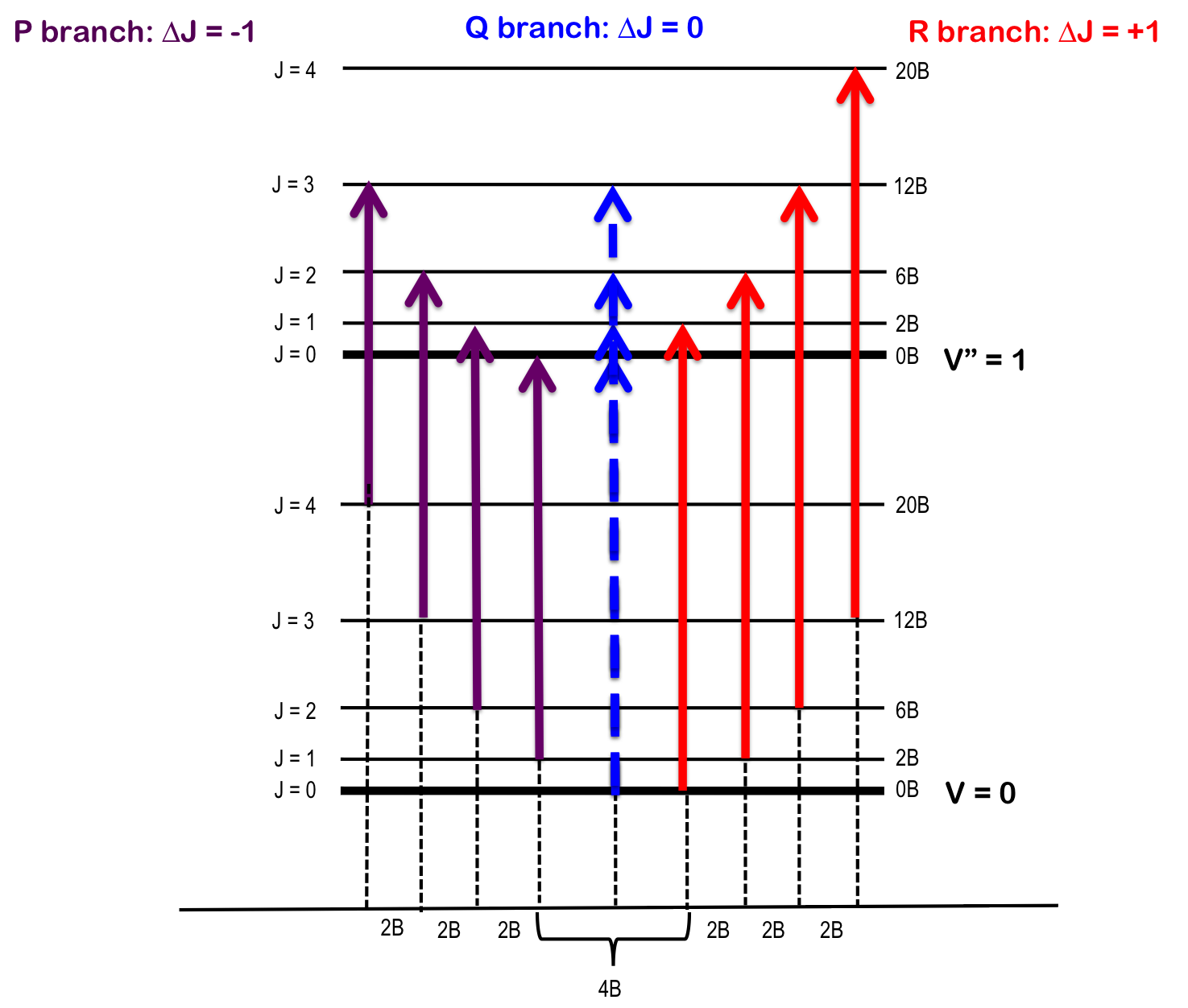
The larger $v$ , the more molecule vibrates, the smaller $<1/r^2>$ , the smaller $B$ .

$\tilde{B}_v=\tilde{B}_e-\tilde{\alpha}(v+\frac{1}{2})$

where $\tilde{B}_e$ is the hypothetical rotation constant with the equilibrium bond length at the bottom of well.

Graphical method

e.g.

$\tilde{R}_J-\tilde{P}_J=2\tilde{B}_1(2J+1)$

Polyatomic

Perpendicular and parallel vibrations

Stretching changes the dipole moment parallel to the principal axis
Bending changes the dipole moment perpendicular to the principal axis

For perpendicular vibrations, the $\Delta J=\pm1$ need not hold! This is due to vibrational angular momentum - when the two degenerate perpendicular modes combine in phase, a circular motion along the principal axis results.

Hence in linear, bending modes, Q branch is seen. Also, $B_1>B_0$ in bending modes.

Lack of Q branch in any one mode indicates the molecule is linear.

Electronic spectroscopy

Different electronic states give different PE curves.

Selection rules

The total transition dipole moment can be separated into electronic and vibrational parts.

Using the independence of the two parts, and the orthogonality of electronic wavefunctions, the expression reduces to

$|<\!\!\psi_E''|\mu_E|\psi_E'\!\!><\!\!\psi_V''|\psi_V'\!\!>|^2$

the second term is called the Franck Condon factor, which measures the overlap between the two vib states.

If the bond length changes, the FC factor is the greatest for $v'>>0$ ; if the bond length is roughly the same, 0-0 transition is the most intense.
The bond length change is predicted by the bond-order of the electronic states.

Photoelectron spectroscopy

Conservation of energy

For atoms,

$KE=h\nu-I_i$

For molecules,

$KE=h\nu-I-\Delta E_{vib}-\Delta E_{rot}$

But note that removing an electron changes the energy of all the remaining electrons, hence not exactly the orbital energy.

Form of atomic spectrum

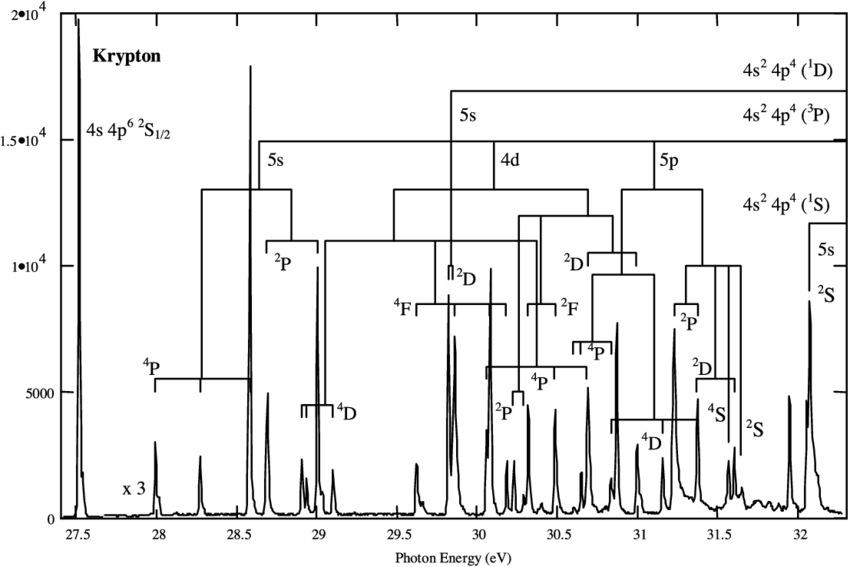
Peaks are labeled with the term symbols of the resulting ions.
Within a term, the relative energies of levels are according to Hund’s 3rd rule.
The degeneracies $2J+1$ is a main contributor of relative intensities of peaks.

Spin-Orbit coupling

The size of spin-orbit coupling is seen on the PES spectrum. Two main factors

The greater the nuclear charge $Z$ , the larger size;
The closer the electron to the nucleus, the larger the interaction.

Molecular spectrum

A progression is seen for each peak, representing the different vibration states in the resulting electronic state.
Within each progression, $\tilde{\omega}$ and $\tilde{\omega}x_e$ can be determined, for that electronic state.

Bond order

We can deduce the change in bond order - or how bonding/antibonding is the orbital that the electron is removed from, through two features.

Number of intense peaks. According to F-C factor, as in electronic spectra.
The $\omega$ value of the resulting bond vibration. The stronger the resulting bond, the larger the gap between peaks in the progression.