Contour Integration
Idea: A powerful method of doing integrals by using the properties of complex functions.
Analytic functions
- To be differentiable at a point, a function must satisfy Cauchy-Riemann.
To be analytic in a region, exists and is continuous in the region; to be analytic at a point, needs to be analytic in a region around the point.
If analytic, and both satisfy 2D-Laplace equation.
Complex Integrals
To do integration on a complex plane, we need to specify a contour - the result may depend on the contour.
Properties
Contours can add up.
Reverse direction gives negative the result.
By parts and substitution applies.
If a contour has length L, then
Cauchy’s theorem
If a function is analytic in a simply-connected domain , then for any simple closed curve in ,
Proof by Green’s theorem in 2D.
Consequence
Deforming a contour does not change the value of integral, as long as it does not cross a singularity.
If has no singularities anywhere, then integrals does not depend at all on the contours.
Residues
The coefficient in the Laurent expansion is the residue of the pole.
Ways to calculate residues*
Direct expansion
Simple pole:
Pole of order N:
L’Hopital’s rule in conjunction with the above.
If is analytic, residue of is .
If has a simple zero, is analytic, residue of is .
Calculus of residues
Residue theorem: f(z) in a simply connected region is analytic except a finite number of poles at , and a simple closed curve encircles the poles in an anticlockwise direction,
Proof by substitute polar, for a small circle around a pole.
Cauchy’s formula
for analytic . Follows directly from residue theorem.
The point at infinity
The is a single point if considering the stereographic projection of the complex plane onto the Riemann sphere.
To study the behaviour at infinity, define a new variable and study its behaviour at 0.
Multivalued functions and branch cuts
A point that cannot be encircled by a curve where the function is continuous and single-valued is called a branch point.
To make a function continuous and single valued, a branch cut is introduced to prevent any curve from encircling that point.
The cut can be any curve from the branch point to infinity.
In some cases, a finite branch cut may be used to connect two branch points. Check by encircling both points.
Branch cuts do not actually matter for integrals not encircling the branch point for .
Choices of contours
Several standard choices are listed below.
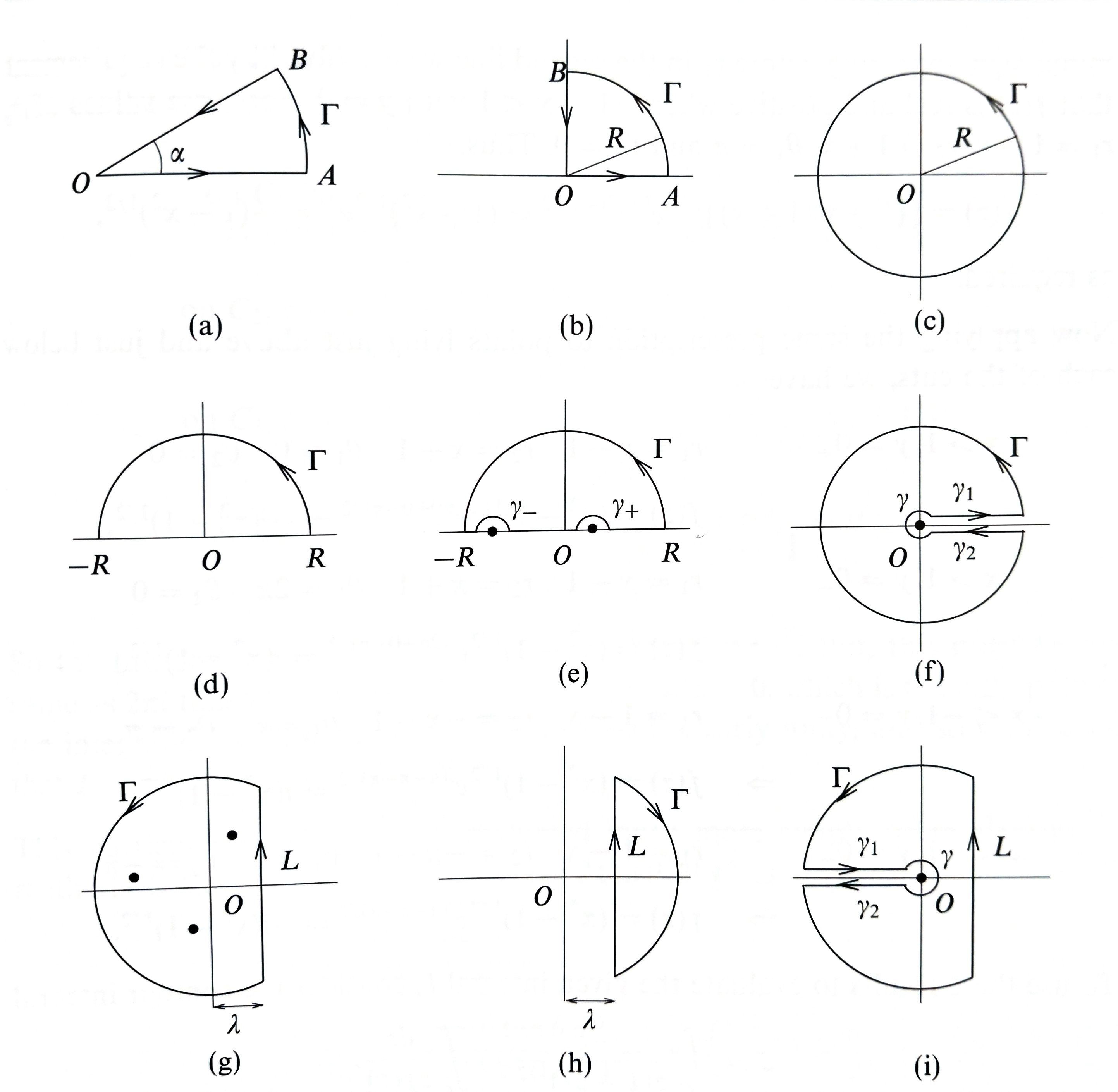
- When evaluating straight lines not on real axis, carefully parameterise .
- For keyholes, make sure the and bits both vanishes (or at least converges). - check their big O
Transformation Methods
Jordan’s lemma
If uniformly (order does not depend on angle) on as , then
Fourier transform methods
- Reduce the order of an ODE/PDE by doing FT.
- In space, express the target function as a product of functions, one of which we know the FT, , the other one we know the original function .
- Either
- realise that in space, the original function is a convolution, so find the anti-FT first. Or;
- find the FT first and do an inverse transform.